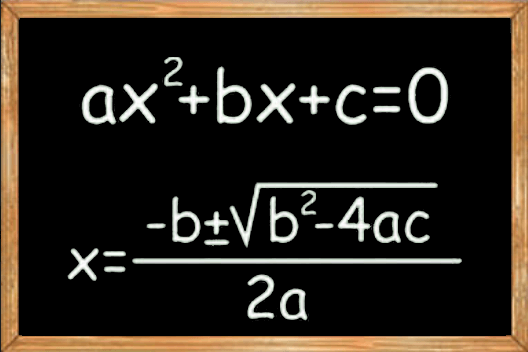The idea of discriminant is extremely important in many areas of mathematics, including algebra, geometry, and even practical applications. Learn everything there is to know about discriminants, why they matter, and how a discriminant calculator can make your life easier. Let’s dive into the nuances and uses of the discriminant calculator, whether you’re a student struggling with algebraic equations or an enthusiast interested in mathematical instruments.
Introduction to the Discriminant
In mathematics, the discriminant is particularly useful when working with quadratic equations. A quadratic equation takes the form ax2 + bx + c = 0, and it is a polynomial equation of the second order. Delta, the Greek letter that represents the discriminant, is calculated using the formula b2 – 4ac.
Understanding Quadratic Equations
Let’s review quadratic equations before getting into the discriminant’s relevance. These equations have practical uses in physics, engineering, and other scientific fields, and they are commonly used to depict parabolic curves.
The Significance of the Discriminant
The discriminant of a quadratic equation can be used to get insight into the characteristics of the equation’s roots. Depending on the number, we can tell if the equation has two separate real roots, a single set of real roots repeated several times, or complex conjugate roots.
Calculating the Discriminant Manually
Manually determining the discriminant requires plugging the quadratic equation’s coefficients (a, b, and c) into the formula = b2 – 4ac. The resultant value of gives information on the properties of the roots of the equation.
Enter the Discriminant Calculator
Manual computations are tedious and error-prone in today’s technologically advanced world. Here’s when the discriminant analysis tool comes in handy. The discriminant of a given quadratic equation may be quickly calculated using this online calculator.
How to Use the Discriminant Calculator
The discriminant calculator may be used with little effort. Simply plug in the coefficients a, b, and c and hit the calculate button to get the discriminant value. This number can be used as a benchmark while studying the equation’s roots.
Real-life Applications of the Discriminant
Discriminant analysis software has many practical uses. In physics, they are used to predict where a projectile will go, and in engineering, they are used to analyze structural vibrations. Discriminants are used in economics as well, to better comprehend supply and demand curves.
Discriminant and Nature of Roots
The discriminant’s significance might shed light on the backstory. If is nonzero, then there are two distinct real roots. If = 0, then there are several instances of real roots. When x is equal to zero, the equation has complex conjugate roots.
Exploring Higher-Degree Equations
The notion of discriminants is not limited to quadratic equations; it may be used to higher-degree polynomial problems as well. Nonetheless, the increasing complexity of the formulae demonstrates the beauty of quadratic equations.
Limitations of the Discriminant
It’s vital to remember that the discriminant doesn’t reveal anything about the roots’ actual values, only their intrinsic characteristics. Finding the precise numbers requires the use of other techniques, such as factoring and completing the square.
Beyond Algebra: Discriminant in Geometry
Interestingly, the idea of discriminants extends well beyond the realm of mathematics. It is in the context of conic sections that they make their first appearance in geometry, providing insight into the form and orientation of curves like circles, ellipses, and hyperbolas.
The Role of Discriminant in Curve Sketching
Curves of quadratic equations can be sketched with the help of discriminant values. The discriminant may be used to find out if the parabola expands out along the x-axis and in what direction.
Discriminant and Optimization Problems
Discriminant values are useful in solving optimisation issues because they assist pinpoint bottlenecks. Points of maximum and lowest value are useful in many disciplines, including economics, engineering, and physics.
The Future of Discriminant Calculators
Discriminant calculators are anticipated to improve in functionality and ease of use as technology develops. They will keep facilitating the mathematical work of students, academics, and professionals.
Conclusion
Finally, the discriminant calculator eases the painstaking analysis of quadratic equations. The discriminant plays an important role in mathematics and beyond, from elucidating the structure of roots to shaping real-world situations. You can count on the discriminant calculator to be there for you whether you’re working through an algebra problem or delving into the fascinating realm of geometry.
Frequently Asked Questions (FAQs)
1. What is a discriminant calculator?
A discriminant calculator is a tool used to determine the roots of a quadratic equation by computing the discriminant of the equation.
2. How does the discriminant influence real-life applications?
One may use the discriminant in physics, engineering, and economics to better understand motion, vibrations, and supply-and-demand scenarios.
3. Can the discriminant calculator handle equations of higher degrees?
Although the idea was first used to quadratic problems, its principles may be applied to polynomial equations of higher degrees, albeit with more complicated formulae.
4. Is the discriminant sufficient to find the exact values of roots?
No, the discriminant only exposes the general kind of roots, not their precise numerical values. For that, you’ll need to resort to techniques like factoring and completing the square.